MVE045 Matematisk analys H20

Jump to today

Kan hända att några länkar funkar inte. Sidan är under bearbetning på det sättet att länkar kommer att uppdateras. Allt ”fast” text (speciellt när det gäller kurslitteratur, Kurs PM, och upplägg) är som den skall vara.

Rösta för video: https://docs.google.com/spreadsheets/d/1FRsaKr6fUATJ9sBntah5GzoYgdlnQXIvA5rjPN9xwI8/edit?usp=sharing

Handledning inför tentamen!!! vi försäkrar minst 15 poäng på tentamen, processen börjar idag

Följ länken: handledning inför tentamen.

Studenter som är anmälda till tentamen

  • Vet inte om det här är "laglig" att lägga ut alla namn så här, så klaga om det stör er på något sätt, så tar jag bort listan (jag var försiktig, det finns inga personnummer, eller email, eller kontakt information).
  • Listan hittas här: studenter som har registrerat sig för tentamen.

Om examination på distans

 Under perioden med distanstentamen på grund av coronapandemin gäller andra regler kring tentamen än normalt.  För aktuell information se sidan: Tentamen under covid-19-pandemin​.  För MVE045 är följande punkter viktiga:

  • På grund av covid-19 sker tentorna under höstterminen på distans. Möjlighet finns för examinator att använda alternativa examinationsformer och jag nyttjar detta 100%.
  • På grund av distans examination det finns ytterligare ett moment som ingår i examinations process – muntlig diskussion.  Sådana muntliga diskussioner kommer att tillämpas bara om examinatorn anser att detta behövs, tex om det finns oklarheter i argumentering (i materialet som lämnades in); typisk exempel kunde vara att en student hoppar över en lång uträkning och bara anger resultat. Alltså, i kort, kan hända att studenter blir kontaktade kring en muntlig diskussion om lösningar som laddades upp saknar argumentation (vill ni slippa det, "tjata" så mycket ni orkar).
  • Tentor som genomförs på distans får vaktas via videoövervakning, och det finns formalia kring hur allt går till (bekanta er med regler, se länken där uppe).
  • Ingen möjlighet att dubbeltentera!
  • Ingen möjlighet att plussa!
  • Examinator har möjlighet att korta ner tentamenstiden: vi gör det inte för MVE045! Tentamen blir 4 timmar lång + 30 minuter för hantering av filer;  2 timmar extra tid för personer som har rätt till förlängd tid + 45 minuter för hantering av filer.
  • Examinationen är inte anonym för tentor som genomförs på distans: Detta nyttjas konstruktivt för enklare återkoppling och eventuella kompletteringar.
  • Alla hjälpmedel tillåtna. (Kom ihåg att samarbete aldrig är tillåtet). Alltså det är ok att använda Mathematica eller liknande. Men, detta ställer extra höga krav på argumentation!
  • Tentamen protokoll (vanligt tid):
    • 14.00 – 18.00: Tentamen – skriv alla svar på pappret;
    • 18.00 – 18.30: Förbereda filer – ta bilder eller skanna och ladda upp i CANVAS. Om problem uppstår skicka över e-mailet till examinatorn (zorank@chalmers.se).
  • Tentamen protokoll (förlängd tid):
    • 14.00 – 20.00: Tentamen – skriv alla svar på pappret;
    • 20.00 – 20.45: Förbereda filer – ta bilder eller skanna och ladda upp i CANVAS. Om problem uppstår skicka över e-mailet till examinatorn (zorank@chalmers.se).

Några allmänna tips:

  • För att skanna (rekommenderades av studenter): CamScanner, Genius Scan, OfficeLens, Adobe Scan
  • "Some students have to use their mobile phone to run Zoom on (because they do not have any other camera) and when they scan their solutions using a scan app Zoom cannot also use the camera and the Zoom video goes black." Om det blir så: Skriv "Scanning solutions" i zoom så att tenta vakter vet.

Kurs-PM

  • På denna sida finns programmet för kursen: föreläsningar, räkneövningar och duggor . Övriga uppgifter, såsom t.ex. kursmål, lärare, kurslitteratur och examination, finns i ett separat kurs-PM.

Program

Kursens schema finns i TimeEdit.

Nytt för i år är att alla föreläsningar kommer att gå över zoom. Räkneövningar derämot kommer att ske i en sal och över zoom. På det sättet alla kan hålla avstånd. Vi kommer att spika ett system med vilka frågor kommer att betraktas efter några räkneövningar när vi alla testar hur allt funkar.

FÖ över zoom: https://chalmers.zoom.us/j/67037636064 Password: 666699

RÖ i HB1: 50 studenter max, hittar man ingen plats går det att följa över zoom

RÖ över zoom: https://chalmers.zoom.us/j/65999883193  Password: 077308

Föreläsningar och rekommenderade övningsuppgifter

 

W1: dugga 1 grunder (1p); W1 detaljer hittas här.

Viktig läsning:

  • P.1, P.2, P.3, P.4, P.5, P.6, P.7

Relevanta problem:

  • P.1:1-45; P.2:alla; P.3:alla; P.4:alla; P.5:alla; P.6:alla, P.7:alla
  • Problem som kommer att diskuteras under RÖ kommer att cirkuleras i förväg (som ppt bilder) och det blir så för varje vecka.

L1 bakgrund/mängder (W1L1 mängder.pdf)

L2 bakgrund/funktioner (W1L2 funktioner.pdf)

L3 bakgrund/funktioner (W1L3 funktioner.pdf)

RÖ 1 & 2:

Lärande mål (efter den här veckan studenter skall kunna):

  • förklara begreppet mängd och operationer med mängder
  • förklara vad det innebär för taltyp om decimaler i ett tal upprepas eller inte
  • känna igen de typiska gymnasiemattematikproblem som mängdlära problem (tex inse att lösningen till ekvation systemet 2x+3y=1, 3x-y=12 är en mängd som representeras av tvärsnittet av två linjen som ekvationer definierar)
  • förklara varför är (-1)(-1)=1, 1+(-2)=1-2, etc.
  • härleda konjugatregeln från distributiva lagen
  • härleda kvadreringsregeln från distributiva lagen
  • för en angiven funktion räkna dess invers och beskriva hur deras grafer är relaterade

 

 

W2: dugga gränsvärden och kontinuitet (1p); W2 detaljer hittas här.

L1 gränsvärdet: grunder

L2 gränsvärdet tillämpningar: kontinuitet (W2-FÖ2 onenote talva.pdf)

L3 derivata grunder

Viktig läsning:

  • L1: 1.2 Limits of functions; 1.3 Limits at infinity and infinite limits; 1.5 The formal definition of Limit
  • L2: 1.4 Continuity
  • L3: 2.1 Tangent Lines and Their Slopes; 2.2 The derivative; 2.3 Differentiation rules

Räkneövningar:

Relevanta problem RÖ1:

  • 1.2:1,17,21,49,65
  • 1.3:1,27,29

Relevanta problem RÖ2:

  • 1.4:1,2,3,7-12,15,17,19, 22, 23
  • 1.5:3,4,7,25-28
  • 2.1: 1, 5, 13, 15, 24
  • 2.2:1-6,11,14,15,17,22,23,,25,26, 27,40,46,48
  • 2.3: 1-30,33-36

Lärande mål (efter den här veckan studenten skall kunna):

  • förklara begreppen gränsvärdet, kontinuitet, och derivata
  • räkna gränsvärden numerisk
  • räkna gränsvärde analytisk med lämpliga tekniker
  • bedöma om en funktion är kontinuerlig eller inte
  • för enklare funktioner räkna derivatan från dess definition

 

W3: dugga 3 – derivata (1p max)

L1 tekniker att hitta derivata (W3-L1 onenote tavla.pdf)

L2 tillämpningar av kedjeregeln och implicit derivata (W3-L2 onenote tavla.pdf)

L3 derivata av komplicerade funktioner: trigonometriska funktioner (W3-L3 onenote tavla.pdf)

RÖ relevanta problem

Viktig läsning:

  • 2.4 the chain rule
  • 2.5 derivatives of trigonometric functions
  • 2.7 using differentials and derivatives
  • 2.9 implicit differentiation
  • 3.1 inverse functions (definition and derivatives of)
  • 3.5 the inverse trigonometric functions and their derivatives

Lärande mål:

  • manipulera komplicerade algebraiska utryck
  • räkna derivatan av komplicerade funktioner
  • räkna derivatan av implicita funktioner
  • bevisa att derivatan (sin x)’ = cos x
  • förklara vad differentialer df och dx betyder
  • förklara varför är det sant att dx+dx2=dx
  • lösa RÖ problem för den aktuella veckan

 

W4: dugga 4 (0.5p max) – derivata tillämpningen

L1 derivata av komplicerade funktioner: exp och log

L2 komplicerade limes med ln x, exp x, och polynomer

L3 Approximationer med polynom och potenser

Viktig läsning:

  • 3.2 Exponential and Logarithmic Functions
  • 3.3 The natural Logarithm and Exponential Functions: TH 1, TH 2, TH3, Logarithmic Differentiation
  • 3.4 Growth and Decay
  • 3.6 Hyperbolic Functions (själv studie, själv studie 1.mp4)
  • 4.1 Related Rates (Example 2) (själv studie)
  • 2.8 the mean value theorem
  • 4.3 indeterminate forms (L’Hopital)
  • 4.9 linear approximations
  • 2.6 higher order derivatives (själv studie)
  • 4.10 Taylor polynomials: T12 Taylor’s Theorem

Relevanta problem:

  • se RÖ pdf för den aktuella vecka
  • 3.2: 1-8, 13, 35, 36
  • 3.3: 1-14, 19-22, 51
  • 3.4: 1-8
  • 3.6: 1-4, 5, 7
  • 4.1: 1-7, 16
  • 4.3:  12, 14, 16
  • 4.9: 1-6, 11, 12
  • 2.6: 1-6, 17
  • 4.10: 1-5, 6, 9, 10

Extra material:

 Videor:

Rekommenderade länkar:

Lärande mål:

  • räkna komplicerade gränsvärde som kräver logaritmering eller L’Hopital regel eller en kombination av dessa
  • approximera en funktion med linjer funktion (första grads polynom)
  • approximera en funktion med en högre grad polynom
  • räkna högre grads derivata
  • avgöra kring vilken punkt en polynom approximation fungerar bäst
  • välja en bra punkt för Taylor utvecklingen beroende på problemet, tex argumentera kring vilken punk man skall approximera sin(x) om designar en räknare, eller sensor, etc.
  • förklara meningen bakom O() notationen
    • kunna avgöra vilken approximation är bättre
    • kunna förhålla sig till notationen utifrån givna praktiska begränsningar, tex att kunna välja den optimala approximationen om flera approximations formler är angivna

 

W5 skulder, derivata diskussion, analysera grafer, Riemann integral

L1 ytterligare derivata tillämpningar

  • 4.10 Taylor polynomials: TH12 (Taylor), DEF 9 Big-O Notation
  • horisontella asymptoter, snedda asymptoter, andra asymptoter (behövs för 4.6 Sketching the graf of a function)
  • 4.2 Finding roots of equations

L2 ytterligare derivata tillämpningar

  • 4.1 Related rates
  • 4.5 Concavity and inflections
  • 4.6 Sketching graphs
  • 4.4 Extreme values
  • 4.8 Extreme value problems

L3 Riemann integral

RÖ relevanta problem

  • W5 RÖ1 derivata tillämpningar approximationer.pdf
  • W5 RÖ2 derivata tillämpningar grafer.pdf
  • 4.1: 1, 2, 3, 4, 12, 13
  • 4.2: 1 (kräver räknare)
  • 4.4: 1-4, 5, 6, 9, 32, 34, 36
  • 4.5: 1-4, 17, 19
  • 4.6: 7, 8, 25, 26
  • 4.8:  1-4, 7, 8, 18
  • 4.10:  1-4, 9, 10
  • 5.2: P1, P8
  • 5.3: P1, P4, P10 (express limit as a definite integral), P11, P15
  • 5.4: P1, P2, P3, P6, P7, P17
  • 5.5: P1, P3, P5, P4, P9, P11, P13, P49, P39, P40, P41, P42, P47 (tips: räkna derivatan av höger och vänster sidan)

Extra material:

Lärandemål

  • approximera funktioner med potensserier
  • numerisk hitta roten av f(x)=0 med Newton-Raphson metoden
  • analysera grafer av funktioner och identifiera viktiga punkter (kritiska, singulära, min, max, etc)
  • formulera och lösa enklare optimerings problem
  • utföra känslighets analys
  • skatta procentändringar med linjär approximation
  • förklara vad Riemann integral betyder
  • förklara ordningen mellan olika summor som används att approximera integralen
  • definiera villkor för att integralen skall finnas

Rekommenderade videor

 

 

W6: dugga 5 (1p max) - integraler

RÖ:

L1 integrations tekniker

Viktig läsning:

  • AD/5 Integration
    • AD/5.5 The fundamental theorem of calculus
    • AD/5.6 The method of substitution

  • AD/6 Techniques of integration

    • AD/6.1 Integration by parts
    • AD/6.2 Integrals of rational functions
    • AD/6.3 inverse substitutions
    • AD/6.4 other methods of evaluating integrals
    • AD/6.6 The trapezoid and midpoint rules
    • AD/6.7 Simpson’s rule

Relevanta problem

  • AFS: 5.5: 1-5, 9, 11, 16, 33, 35, 38, 39, 45 (tenta 46), 49, 50 (tenta), 51 (tenta)
  • 5.6: 1, 3, 5(tenta), 6(tenta), 9(tenta), 11, 12 (tenta), 17, 26, 28(tenta), 50, 51 (tenta, MVG) 
  • partiell integration: 6.1.1, 6.1.2, 6.1.5, 6.1.31, 6.1.32
  • rationella funktioner: 6.2.12, 6.2.22
  • substitutions tekniker: 6.3.1, 6.3.3, 6.3.9, 6.3.16, 6.3.24

Extra material

Lärandemål

  • beräkna integraler analytiskt och numeriskt
  • föreslå substitutioner för enklare integraler
  • för en angiven substitution utföra analytiska steg som följer
  • kunna jämföra noggrannhet av olika numeriska integrations tekniker
  • kunna använda tabeller med derivator och integraller

Rekommenderade videon

Basic Integration... How? (NancyPi) (intro, men kanske lite för enkelt)

How to Integrate Using U-Substitution (NancyPi) (variable byte)

Integration by Parts... How? (NancyPi) (goda exempel/råd för partielintegration)

integral av 1/sinx

L2 Tillämpningar av integraler: längder av kurvor i 2D, ytor i 2D

Viktig läsning:

  • AD/5.7 Areas of plan region
  • AD/7.3 Arc Length and Surface Area

Relevanta problem

  • längder av kurvor: AD/7.3.1, 7.3.2, 7.3.7, 7.3.8
  • enkla ytor: AD/5.7.1, 5.7.2, 5.7.3, 5.7.4
  • komplicerade ytor: AD/5.7.17, 5.7.18

Lärandemål

  • kunna tillämpa integralberäkningar på ytor i 2D
  • kunna tillämpa integralberäkningar på längder av kurvor i 2D

L3 Tillämpningar av integraler: ytor och volymer i 3D som definieras med roterande funktioner

Viktig läsning:

  • AD/7.1 Volumes by slicing – solids of revolution
  • AD/7.2 More volumes by slicing
  • AD/7.3 Arc length and surface area
    • Areas of Surfaces of Revolution

Relevanta problem

  • volumes by slicing: AD/7.1.1, 7.1.2, 7.2.1, 7.2.2
  • volumes by rotating graph: AD/7.3.22, 7.3.23,7.3.26

Lärandemål

  • kunna räkna längder av kurvor (i 2D), ytor (3D) och volymer (3D) av geometriska objekt som definieras med en graf f(x) som roteras, eller en yta A(x) som förflyttas
  • för en given geometrisk objekt, kunna identifiera grafen som beskriver objektet

 

W7: dugga 6 (0.5p max) – komplexa tal och differentiella ekvationer

RÖ:

L1 enkla differentiella ekvationer

Viktig läsning:

  • AD/18.1 Classifying differential equations
  • AD/7.9 First order differential equations
  • AD/18.4 Second order differential equations
  • AD/18.5 Linear differential equations with constant coefficients
  • AD/18.6 Non-homogeneous linear equations
  • AD/3.7 Second-order linear DEs with constant coefficients

Relevanta problem

  • AD/18.1: 1-10 (beskriva DE: ordningen, linjär/icke linjär, etc)
  • AD/18.1:11-12 (verifiera lösningar, är summan av lösningar en lösning?)
  • AD/18.1.13 (den harmoniska oscillatorn)
  • AD/18.1.14 (hyperboliska funktioner)
  • AD/18.1.16 (den karakteristiska ekvationen med reella lösningar)
  • AD/18.1.17 (driven harmonisk oscillatorn + att kombinera homogen och partikulär lösning)
  • AD/18.1.18 (att kombinera homogen och partikulär lösning)
  • AD/3.7:1-12 (general solution to the second order DE)
  • AD/3.7:13-15 (initial value problems, second order DE)
  • AD/3.7:26-28 (harmonic oscialltor)
  • AD/7.9:1-10 (separable equations) <= detta är viktig, gör så många ni kan för att utveckla känslan
  • AD/7.9:11-16 (metod II, generellt lösning – fria konstanter)
  • AD/7.9:17-20 (metod II, lösning med begynnelsevillkor – inga fria konstanter)

Extra material:

Lärandemål: Studenter skall kunna lösa första grads differentiella ekvationer analytiskt när det är möjligt. För det andra och högre grads linjära ekvationer med konstanta koefficienter, studenter förväntas kunna diskutera antal och typer av möjliga lösningar. För andra grads ekvationer, man skall ha den operativa kunskapen att lösa vilken problem som helst, med eller utan begynnelse villkor. För andra grads ekvationer med icke konstanta koefficienter det enda man skall kunna är att känna till och använda den allmänna principen att linjär kombination av lösningar är också en lösning, och att det finns två oberoende lösningar. Sammanlagt, lärandemål är:

  • att kunna lösa enklare differentiella ekvationer
  • Att kunna känna igen separabla diff ekvationer av första grad och omvandla till integral problem
  • Att lösa (de som kan fixas på detta sätt) första grads DE med icke konstant koefficienter
  • Att lösa vilken som helst andra grads DE med konstanta koefficienter

L2 Komplexa tal och tillämpningar

Viktig läsning:

  • grunder: AD/Appendix I
    • definition: z=x+iy
    • algebra: z1*z2 och z1/z2,
    • tekniker: Re, Im, z och z*, Abs(z)
  • Euler formula "bevis": AD/Appendix II/The exponential function
  • den polära formen av ett komplex tal: AD/Appendix I
  • tillämpningar till DE
  • samband mellan trigonometriska och hyperboliska funktioner: AD/9 Sequences, series, and powers/Other Maclaurin and Taylor series
  • algebraiska ekvationer med komplexa tal: hitta högre rötter, hitta andra roten, omvandla mellan x+iy och den polära formen:  AD/Appendix I/Roots of complex numbers

Relevanta problem

  • AD/Appendix I: 1-4; 5-12;16,17,24,25,40,41,51,52
  • AD/Appendix II: 17, 19, 21, 23*, 27-31

Extra material

Lärandemål

  • Komplexa tal algebran är ett viktigt verktyg som används att lösa linjära differentiella ekvationer. Lärande mål är att bemästra alla praktiska tekniker att hantera komplexa tal i en differential ekvation kontext.

Rekommenderade videon

Eulers formula bevis 1

Eulers formula bevis 2 (Taylor Series)

Eulers formula bevis 3 (A cool proof)

L3 tentamen genomgång

  • tentor är olika men alla har samma teman
  • svårighetsgrad 3:
    • komplexa tal
    • differentialer dx, df, linjär approximation
    • kontinuitet
    • enklare implicit derivata problem (polynomer, arctan, arccot, arccos, etc)
    • ”derivarberhet”
    • gränsvärdet: L’Hopital
    • enkla integraler
    • att derivera med kedjeregel
    • Taylor utveckling
    • enkla differentiella ekvationer
  • svårighetsgrad 4
    • svårare integraler
    • svårare gränsvärdet
    • tangenten in en punkt av en graf
    • medel komplicerade differentiella ekvationer: separations teknik
    • enkla ytor med roterande grafer
    • linjära DE grad 2 med konstanta koefficienter
  • svårighetsgrad 5
    • svårare problem som kräver att olika analys tekniker används sammtidigt
    • komplicerade gränsvärden
    • komplicerade derivata
    • optimerings problem

Extra material:

Lärandemål:

  • Ta del av på vilket sätt man skall svara under tentamen
  • Ha en uppfattning av hur ett ”bra” svar ser ut
  • Ha en uppfattning av hur ett ”dålig” svar ser ut

 

W8 sammanfattning

L1 sammantagning

Extra material:

Lärandemål

  • Förklara kursens upplägg och idén bakom kursen (triagneln mallen)
  • Förklara varför olika ämne i kursen diskuterades i en vis ordning
  • Förklara hur man blir betygsätt
    • Hur den skriftliga tentamen rättas
    • Hur dugga bonus poäng kombineras med tentamenspoäng

 

Efter varje vecka delas separata dokument ut med detaljerad information om kursen. Dessa filer kan nås genom länken MVE045 HT 2019 shared, och allt övrigt utdelat material kan nås igenom samma länk. Tex leta efter dokument med filnamn ”WX-LY.pdf” där X är veckotal (1, 2, 3, etc) och Y säger vilken lektion (1, 2, 3, etc) informationen handlar om. Överblick över hela kursens innehåll  hittas i mve045 kurs översikt v4.pdf.

Formel blad

formel blad.pdf

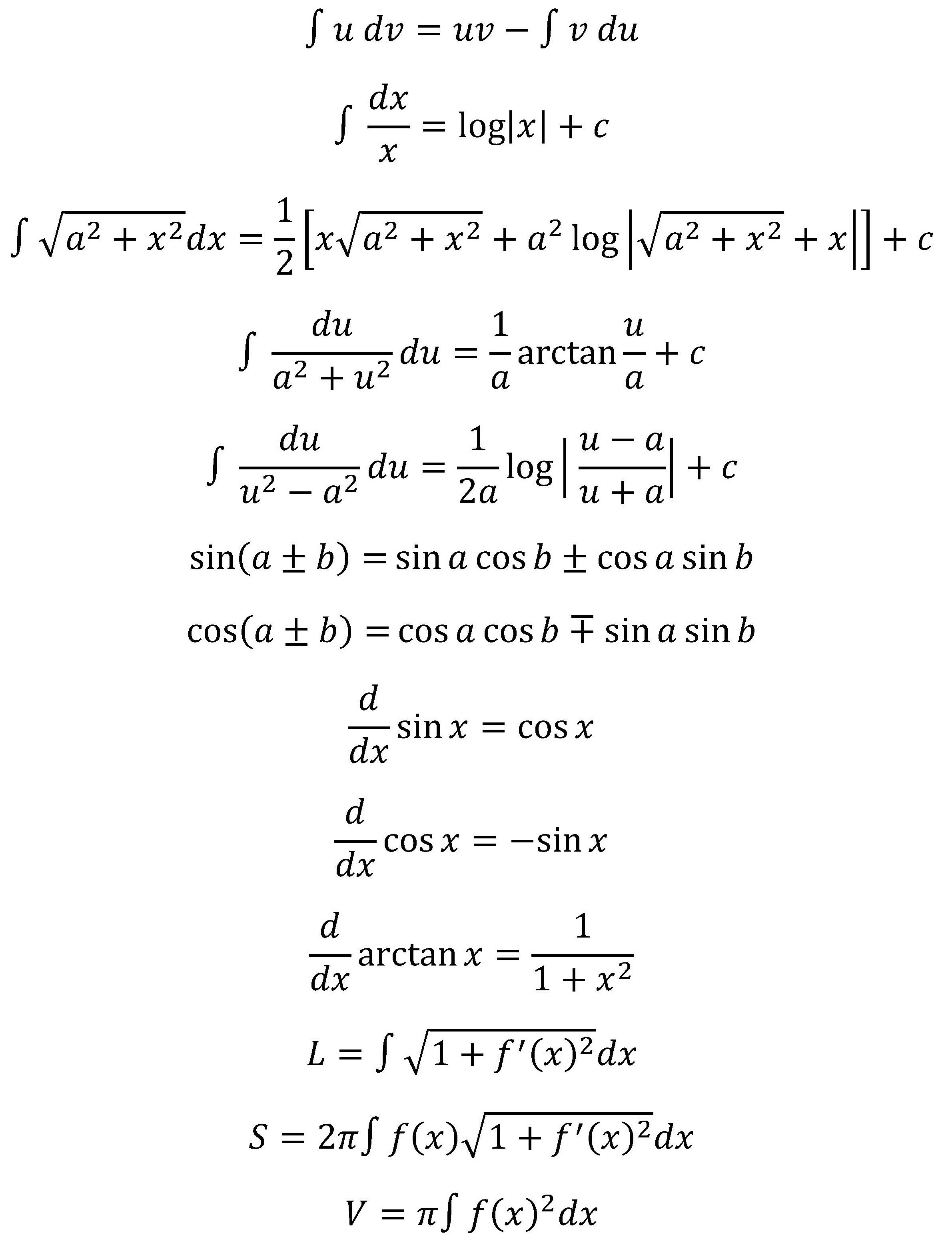
formel blad.jpg

 

Tillbaka till toppen

Datorlaborationer

Inga obligatoriska datorlaborationer eller datorövningar ingår i kursen.

Referenslitteratur för Matlab:

  1. Material utvecklat av MV som ger en kortfattad introduktion till Matlab
  2. Programmering med Matlab,  Katarina Blom. Ger en introduktion till Matlab och lär ut grunderna i programmering med Matlab. Rekommenderas varmt för dig som är nybörjare både vad gäller programmering och Matlab.
  3. Learning MATLAB, Tobin A. Driscoll. Ger en kortfattad introduktion till Matlab till den som redan kan programmera. Finns som e-bok på Chalmers bibliotek.
  4. Physical Modeling in MATLAB 3/E, Allen B. Downey
    Boken är gratis att ladda ner från nätet. Boken ger en introduktion för dig som inte programmerat förut. Den täcker grundläggande MATLAB-programmering med fokus på modellering och simulation av fysikaliska system.

 

Tillbaka till toppen

Duggor

Duggor är frivilliga, dock uppmuntras studenter starkt att göra dessa. Duggor ges i elektronisk form, ungefär en gång per vecka. Kan nås igenom CANVAS portalen. Max antalet duggapoäng är 5.

Tillbaka till toppen

Course summary:

Date Details Due