VIKTIG: Detta är den gamla kurshemsidan och den borde vara avstängt från CANVAS. Att ni kan se den är ett misstag i CANVAS systemet. Använd den andra sidan som har HT2020 i titeln.
Kurs-PM
På denna sida finns programmet för kursen: föreläsningar, räkneövningar och duggor . Övriga uppgifter, såsom t.ex. kursmål, lärare, kurslitteratur och examination, finns i ett separat kurs-PM.
Program
Kursens schema finns i TimeEdit.
Föreläsningar och rekommenderade övningsuppgifter
| W1: dugga 1 grunder (1p, avrundning med G/U) |
|
L1 bakgrund/mängder
|
| L2 bakgrund/funktioner |
|
L3 bakgrund/funktioner
|
| W3: dugga 3 – derivata (1p max) |
| L1 tekniker att hitta derivata |
| L2 tillämpningar av kedjeregeln och implicit derivata |
|
L3 derivata av komplicerade funktioner: trigonometriska funktioner
|
| W5 skulder, derivata diskussion, analysera grafer, Riemann integral |
| L1 ytterligare derivata tillämpningar |
|
L2 ytterligare derivata tillämpningar
|
|
L3 Riemann integral
Viktig läsning:
- AD/5.2 Areas as limits of sums
- AD/5.3 The definite integral
- AD/5.4 Properties of the definite integral
- AD/5.5 The fundamental theorem of calculus
- AD/5.6 The method of substitution
- AD/5.7 Areas of plan regions
Relevanta problem
- AD/5.2: P1, P8
- AD/5.3: P1, P4, P10 (express limit as a definite integral), P11, P15
- AD/5.4: P1, P2, P3, P6, P7, P17
- AD/5.5: P1, P3, P5, P4, P9, P11, P13, P49, P39, P40, P41, P42, P47 (tips: räkna derivatan av höger och vänster sidan)
Lärandemål
- förklara vad Riemann integral betyder
- förklara ordningen mellan olika summor som används att approximera integralen
- definiera villkor för att integralen skall finnas
Rekommenderade videor
|
| W6: dugga 5 (1p max) - integraler |
|
L1 integrations tekniker
Viktig läsning:
Relevanta problem
- partiell integration: 6.1.1, 6.1.2, 6.1.5, 6.1.31, 6.1.32
- rationella funktioner: 6.2.12, 6.2.22
- substitutions tekniker: 6.3.1, 6.3.3, 6.3.9, 6.3.16, 6.3.24
Lärandemål
- beräkna integraler analytiskt och numeriskt
- föreslå substitutioner för enklare integraler
- för en angiven substitution utföra analytiska steg som följer
- kunna jämföra noggrannhet av olika numeriska integrations tekniker
Rekommenderade videon
Basic Integration... How? (NancyPi) (intro, men kanske lite för enkelt)
How to Integrate Using U-Substitution (NancyPi) (variable byte)
Integration by Parts... How? (NancyPi) (goda exempel/råd för partielintegration)
integral av 1/sinx
|
|
L2 Tillämpningar av integraler: längder av kurvor i 2D, ytor i 2D
Viktig läsning:
- AD/5.7 Areas of plan region
- AD/7.3 Arc Length and Surface Area
- AD/7.4 Mass, Moments, and Centre of Mass
- AD/7.5 Centroids
Relevanta problem
- längder av kurvor: AD/7.3.1, 7.3.2, 7.3.7, 7.3.8
- enkla ytor: AD/5.7.1, 5.7.2, 5.7.3, 5.7.4
- komplicerade ytor: AD/5.7.17, 5.7.18
- centrum av massan med varierande täthet: AD/7.4.1, 7.4.2
- centrum av massan med konstant täthet: AD/7.5.1, 7.5.2, 7.5.4, 7.5.13, 7.5.14
Lärandemål
- kunna tillämpa integralberäkningar på ytor i 2D
- kunna tillämpa integralberäkningar på längder av kurvor i 2D
- kunna tillämpa integralberäkningar på centrum av massan
|
|
L3 Tillämpningar av integraler: ytor och volymer i 3D som definieras med roterande funktioner
Viktig läsning:
- AD/7.1 Volumes by slicing – solids of revolution
- AD/7.2 More volumes by slicing
- AD/7.3 Arc length and surface area
- Areas of Surfaces of Revolution
Relevanta problem
- volumes by slicing: AD/7.1.1, 7.1.2, 7.2.1, 7.2.2
- volumes by rotating graph: AD/7.3.22, 7.3.23,7.3.26
Lärandemål
- kunna räkna längder av kurvor (i 2D), ytor (3D) och volymer (3D) av geometriska objekt som definieras med en graf f(x) som roteras, eller en yta A(x) som förflyttas
- för en given geometrisk objekt, kunna identifiera grafen som beskriver objektet
|
| W7: dugga 6 (0.5p max) – komplexa tal och differentiella ekvationer |
|
L1 enkla differentiella ekvationer
Viktig läsning:
- AD/18.1 Classifying differential equations
- AD/7.9 First order differential equations
- AD/18.4 Second order differential equations
- AD/18.5 Linear differential equations with constant coefficients
- AD/18.6 Non-homogeneous linear equations
- AD/3.7 Second-order linear DEs with constant coefficients
Relevanta problem
- AD/18.1: 1-10 (beskriva DE: ordningen, linjär/icke linjär, etc)
- AD/18.1:11-12 (verifiera lösningar, är summan av lösningar en lösning?)
- AD/18.1.13 (den harmoniska oscillatorn)
- AD/18.1.14 (hyperboliska funktioner)
- AD/18.1.16 (den karakteristiska ekvationen med reella lösningar)
- AD/18.1.17 (driven harmonisk oscillatorn + att kombinera homogen och partikulär lösning)
- AD/18.1.18 (att kombinera homogen och partikulär lösning)
- AD/3.7:1-12 (general solution to the second order DE)
- AD/3.7:13-15 (initial value problems, second order DE)
- AD/3.7:26-28 (harmonic oscialltor)
- AD/7.9:1-10 (separable equations) <= detta är viktig, gör så många ni kan för att utveckla känslan
- AD/7.9:11-16 (metod II, generellt lösning – fria konstanter)
- AD/7.9:17-20 (metod II, lösning med begynnelsevillkor – inga fria konstanter)
Lärandemål: Studenter skall kunna lösa första grads differentiella ekvationer analytiskt när det är möjligt. För det andra och högre grads linjära ekvationer med konstanta koefficienter, studenter förväntas kunna diskutera antal och typer av möjliga lösningar. För andra grads ekvationer, man skall ha den operativa kunskapen att lösa vilken problem som helst, med eller utan begynnelse villkor. För andra grads ekvationer med icke konstanta koefficienter det enda man skall kunna är att känna till och använda den allmänna principen att linjär kombination av lösningar är också en lösning, och att det finns två oberoende lösningar. Sammanlagt, lärandemål är:
- att kunna lösa enklare differentiella ekvationer
- Att kunna känna igen separabla diff ekvationer av första grad och omvandla till integral problem
- Att lösa (de som kan fixas på detta sätt) första grads DE med icke konstant koefficienter
- Att lösa vilken som helst andra grads DE med konstanta koefficienter
|
|
L2 Komplexa tal och tillämpningar
Viktig läsning:
- grunder: AD/Appendix I
- definition: z=x+iy
- algebra: z1*z2 och z1/z2,
- tekniker: Re, Im, z och z*, Abs(z)
- Euler formula "bevis": AD/Appendix II/The exponential function
- den polära formen av ett komplex tal: AD/Appendix I
- tillämpningar till DE
- samband mellan trigonometriska och hyperboliska funktioner: AD/9 Sequences, series, and powers/Other Maclaurin and Taylor series
- algebraiska ekvationer med komplexa tal: hitta högre rötter, hitta andra roten, omvandla mellan x+iy och den polära formen: AD/Appendix I/Roots of complex numbers
Relevanta problem
- AD/Appendix I: 1-4; 5-12;16,17,24,25,40,41,51,52
- AD/Appendix II: 17, 19, 21, 23*, 27-31
Lärandemål
Rekommenderade videon
Eulers formula bevis 1
Eulers formula bevis 2 (Taylor Series)
Eulers formula bevis 3 (A cool proof)
|
|
L3 tentamen genomgång
- tentor är olika men alla har samma teman
- för betyg 3:
- kontinuitet
- ”derivarberhet”
- gränsvärdet: L’Hopital
- enkla integraler
- komplexa tal
- att derivera med kedjeregel
- enkla implicit derivatan (arctan, arccot, arccos)
- differentialer (du,dx)
- Taylor utveckling
- enkla differentiella ekvationer
- för betyg 4
- svårare integraler
- svårare gränsvärdet
- tangenten in en punkt av en graf
- medel komplicerade differentiella ekvationer: separations teknik
- enkla ytor med roterande grafer
- för betyg 5
- linjära DE grad 2 med konstanta koefficener
- andra komplexa problem
Lärandemål:
- Ta del av på vilket sätt man skall svara under tentamen
- Ha en uppfattning av hur ett ”bra” svar ser ut
- Ha en uppfattning av hur ett ”dålig” svar ser ut
- Att kunna förklara examinations modell (portfolio based assessment)
- Känna till uppdelning i separata moduler uppdelade i olika svårighetsgrader
- Specificera typiska ämne som krävs för betyg 3
- Specificera typiska ämne som krävs för betyg 4
- Specificera typiska ämne som krävs för betyg 5
|
| W8 sammanfattning |
|
L1 sammantagning
Förankring av visa viktiga tekniker/kunskaper:
- integraler med svårare variabel byte
- TU i oändligheten
- ytan av en roterande graf
- sh’’(x)-sh(x)=0, y’’(x)-y(x)=0, y’’(x)-4y(x)=0
- ∫dx/x=ln|x|+c; absolut belopp!
- TU i oändligheten
- betydelsen: rita grafen av f(x) och approximationen och jämför i oändligheten
- när skall man använda den?
- finns det fall när det går inte att använda den?
- volymer och ytor med roterande grafer: mysterium av dS
- varför dS=2*Pi*f(x)*dh och inte dS=2*Pi*f(x)*dx?
- några djupa analys frågor
- om villkor för deriverbart
- från första principer (definitionen av derivatan)
- kontinuitet + existens av gränsvärdet av f'(x)
Lärandemål
- Förklara kursens upplägg och idén bakom kursen (förbereda för framtiden: yrkesliv vs fortsätta studier)
- Förklara varför olika ämne i kursen diskuterades i en vis ordning
- Förklara hur man blir betygsätt
- Hur den skriftliga tentamen rättas
- Hur dugga bonus poäng kombineras med tentamenspoäng
|
Efter varje vecka delas separata dokument ut med detaljerad information om kursen. Dessa filer kan nås genom länken MVE045 HT 2019 shared, och allt övrigt utdelat material kan nås igenom samma länk. Tex leta efter dokument med filnamn ”WX-LY.pdf” där X är veckotal (1, 2, 3, etc) och Y säger vilken lektion (1, 2, 3, etc) informationen handlar om. Överblick över hela kursens innehåll hittas i mve045 kurs översikt v4.pdf.
Formel blad
formel blad.pdf
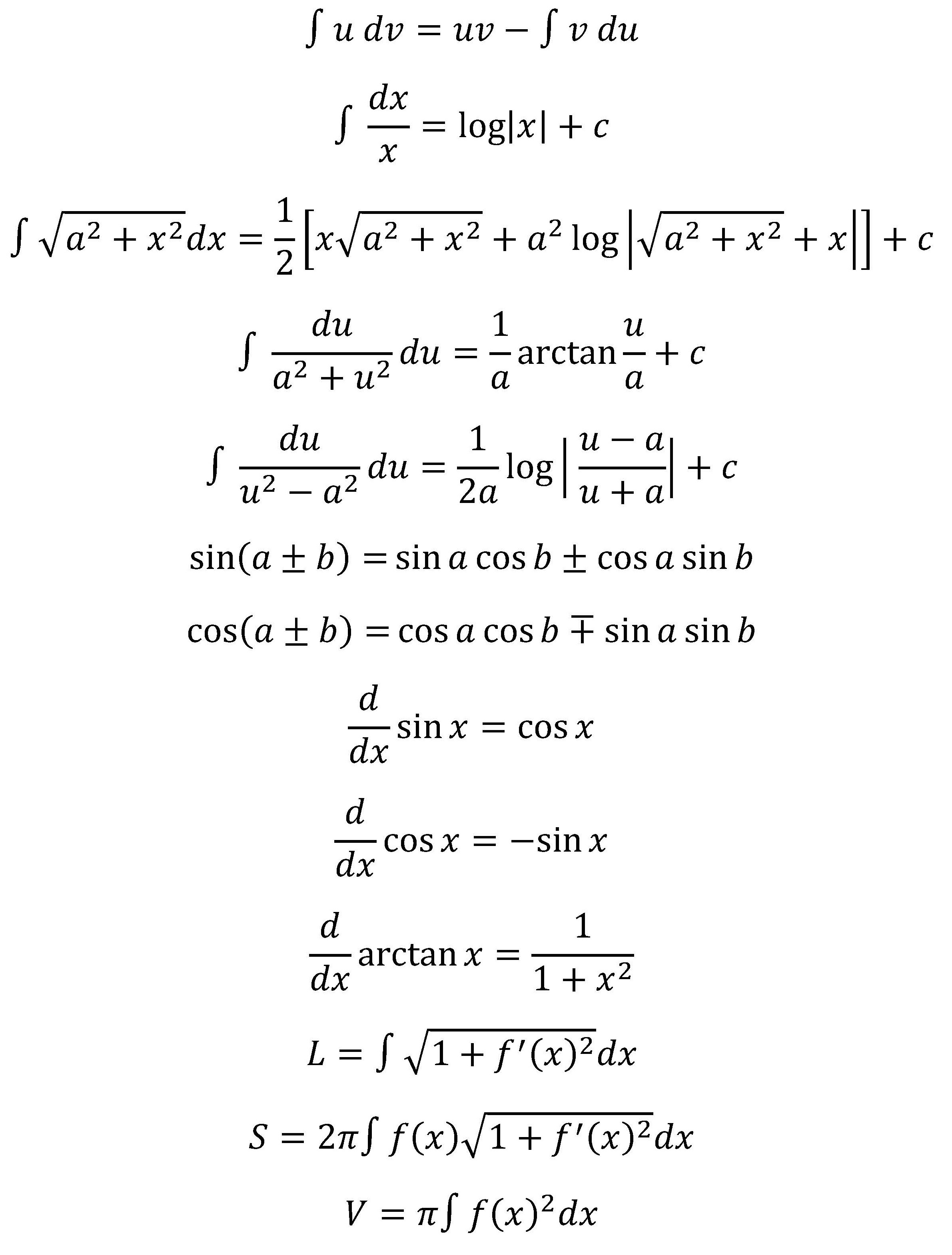
Tillbaka till toppen
Datorlaborationer
Inga obligatoriska datorlaborationer eller datorövningar ingår i kursen.
Referenslitteratur för Matlab:
-
Material utvecklat av MV som ger en kortfattad introduktion till Matlab
-
Programmering med Matlab, Katarina Blom. Ger en introduktion till Matlab och lär ut grunderna i programmering med Matlab. Rekommenderas varmt för dig som är nybörjare både vad gäller programmering och Matlab.
-
Learning MATLAB, Tobin A. Driscoll. Ger en kortfattad introduktion till Matlab till den som redan kan programmera. Finns som e-bok på Chalmers bibliotek.
-
Physical Modeling in MATLAB 3/E, Allen B. Downey
Boken är gratis att ladda ner från nätet. Boken ger en introduktion för dig som inte programmerat förut. Den täcker grundläggande MATLAB-programmering med fokus på modellering och simulation av fysikaliska system.
Tillbaka till toppen
Duggor
Duggor är frivilliga, dock uppmuntras studenter starkt att göra dessa. Duggor ges i elektronisk form, ungefär en gång per vecka. Kan nås igenom CANVAS portalen. Max antalet duggapoäng är 5.
Tillbaka till toppen
The syllabus page shows a table-oriented view of course schedule and basics of
course grading. You can add any other comments, notes or thoughts you have about the course
structure, course policies or anything else.
To add some comments, click the 'Edit' link at the top.
Course summary:
Course Summary
| Date |
Details |
Due |
|
|